Resultats del concurs
La
coordinació de la XIV Olitele, després d'incorporar a la base de dades
les puntuacions dels problemes 10 i 11 i d'analitzar les puntuacions
finals que en resulten, ha proposat a la SCM, que hi ha donat el seu
acord:
- distingir com a premiades les persones que superen els 46 punts sobre el màxim de 48 punts que es podien obtenir
- atorgar diploma de menció als concursants amb més de 41 punts
- publicar a la web els noms dels que superen els 36 punts
Premis de la XIV Olitele
Raquel Trull Báguena,
alumna de 1r de batxillerat de
l'Institut Jaume Vicens Vives de Girona, amb 47,8
punts
Roger Lidón Ardanuy,
alumne de 4t d'ESO de les
Escoles Minguella, de Badalona, amb 47,2 punts
Hugo Lladró Prats,
alumne de 1r de batxillerat de
l'IES Francisco Figueras Pacheco, d'Alacant, amb 47
Roger Bargalló Roselló
alumne de 1r de batxilerat de l'Institut Jaume Vicens Vives, de Girona, amb 46,9 punts
Abel Salinas Sellas
alumne de 1r de batxillerat d'Aula Escola Europea, de Barcelona, amb 46,8 punts
Mencions especials de la XIV Olitele
Laura Guberna Arraiza
alumna de 1er de batxillerat d'Aula Escola Europea, de Barcelona, amb 45,5 punts
Jorge Rico Esteban
alumne de 2n de batxillerat de l'IES Vicent Castell i Doménech, de Castelló, amb 44 punts
Carlos González Bueno
alumno de 2º de bachillerato del Colegio Sta. Teresa de Jesús, de Salamanca, amb 43,2 punts
Candela Hernández Domingo
alumna de 1r de batxillerat de SEK International School-Catalunya, de La Garriga, 43,1 punts
Eva Montseinos Ginés
alumna de 4t d'ESO del Casal dels Àngles, de l'Hospitalet de Llobregat, amb 42,5 punts
Alèxia Escudero Ribó
alumna de 4t d'ESO de l'Institut Morelló, d'Esterri d'Àneu, amb 42,1 punts
Helena Folia Cots
alumna de 4t d'ESO de l'Institut Jaume Balmes, de Barcelona, amb 41,5 punts
La relació d'altres concursants que han superat els 36 punts en la XIV Olitele la componen.
Pablo Rodríguez Manzano (4t ESO, Sagrat Cor Esclaves, Barcelona), 39,3 punts;
Flavià Serret Martí (1r batx, Institut Manuel de Pedrolo,
Tàrrega) i Ruben Carpenter (4t ESO, IE Costa i Llobera,
Barcelona), 39,3 punts; Kristina Galieva (2n batx, Escola Betània-Patmos, Barcelona), 38,4 punts; Guillem Pastor Salvador (4t ESO, Institut Banús, Cerdanyola del Vallès), 37 punts; Arnau Pino Jacomet (3r ESO, IES Montilivi, Girona), 36,9 punts, i Pau Martí Biosca (1r batx, Institut Jaume Vicens Vives, Girona), 36,8 punts.
- Volem fer
arribar una felicitació ben efusiva al conjunt de concursants,...
- de manera molt concreta a les noies i els nois de l'ESO que apareixen el les relacions de concursants destacats
- a tots
els que van respondre els nou problemes de resposta concreta i, en
especial, als que a més han enviat respostes molt ben treballades als
problemes d'explicar.
i, alhora ens felicitem per la diversitat geogràfica de les persones que hem esmentat.
Convocatòria
i instruccions
- La
SCM convoca,
per catorzè any consecutiu, una activitat telemàtica de resolució de
problemes adreçada a alumnes dels darrers cursos de la secundària, que
es
desenvoluparà durant els mesos de novembre i desembre, d'acord amb
les instruccions següents
Instruccions
per al desenvolupament del XIV concurs Olitele
- El concurs s'adreça a alumnes de batxillerat o cicles
formatius.
- Excepcionalment poden participar alumnes de l'ESO. En
aquest cas convé que els ho hagi suggerit una
professora o d'un professor del centre i que tinguin present quins són
els destinataris a que s'adreça prioritàriament el concurs. .
- El
concurs es proposa com una activitat individual per a alumnes dels
nivells
indicats. Per això es demana a les persones que participin que
respectin l'esperit d'aquest concurs i no cerquin ajuts "fora de
concurs".
- La
participació en aquest concurs telemàtic, XIV Olitele, pot
donar idees per a la prova Cangur i també algunes per a preparar
l'Olimpíada
Matemàtica, però l'objectiu de cada proposta és diferent i per això la
participació
en cadascun d'aquests concursos és independent dels altres. .
- La XIV Olitele
consta de 12
problemes
- A més del problema
0, ja comentat:..
- Hi
ha uns altres 8
problemes de resposta concreta (numèrica o d'altres
tipus). Quan s'enviï la solució el formulari indicarà si és o
no correcta
i, en cas que no ho sigui, es disposarà d'un segon intent, amb les
puntuacions que s'indiquen a la taula per al primer intent i la meitat
per al segon. Pot
haver-hi algunes excepcions a aquest procediment si en la solució del
problema es demana una expressió literal; oportunament s'avisaria.
- Finalment, per
als tres problemes que completen els 12 del concurs
caldrà enviar, en un fitxer .PDF,
un
raonament que porti a la solució. Per a això només hi haurà una
oportunitat.
- Per a
facilitar la tasca dels participants, combinant-la amb les diverses
activitats escolars, el termini per a enviar les respostes s'allarga
des de la publicació (un divendres) fins que es tanca el termini de
resposta (habitualment un dilluns, 10 dies després; és a dir amb dos
caps de setmana dintre del termini; amb un parell d'excepcions). Per coordinar
el calendari, la publicació de cada parell
d'enunciats es farà abans que acabi el termini de presentació de
respostes dels dos anteriors.
- Per als "problemes
d'explicar" els terminis són més amplis i no comencen necessàriament en
divendres ni acaben en
dilluns.
Enunciat
del problema 0.
- Aquest
"problema 0" és el
primer problema del concurs. Haureu de donar la resposta com un
nombre natural, sense separador de milers.
- L'encert
dóna 2 punts, o, en cas d'encert al segon intent dóna 1
punt.
- És
bo de saber que
encara que no
s'encerti el problema 0, naturalment que es pot continuar la
participació en el concurs.
|
|
Tots
els participants i altres persones interessades podran enviar
observacions, comentaris, suggeriments,
que (en cas que es creguin d'interès general) podran ser publicats en
aquesta pàgina.
També podeu consultar "dubtes matemàtics", que aquest concurs també té
com a
objectiu ajudar en la preparació matemàtica del jovent.
Atenció!!! Com
a norma general, si teniu dubte en algun enunciat...consulteu!
Veureu que habitualment contestem ben ràpid!
per
a contactar amb
l'organització.
| Problema |
Puntuació (*) |
Publicació |
Termini
de resposta |
|
| 0 |
2 punts |
28 d'octubre |
16 de novembre |
Enunciat
Termini de resposta tancat
|
| 1 |
2 punts |
13 de novembre
|
23
de novembre
|
Enunciat
Termini de resposta tancat
|
| 2 |
3 punts |
13 de novembre
|
23 de novembre
|
Enunciat
Termini de resposta tancat
|
| 3 |
2 punts |
20 de novembre |
30 de novembre |
Enunciat
Termini de resposta tancat
|
4
|
3 punts |
20 de novembre |
30 de novembre |
Enunciat
Termini de resposta tancat
|
5
|
3 punts
|
27 de novembre
|
8 de desembre
|
Enunciat
Termini de resposta tancat
|
6
|
4 punts
|
27 de novembre
|
8 de desembre
|
Enunciat
Termini de resposta tancat
|
| 7 |
(**)
(7 punts) |
28 de novembre
|
14 de desembre
|
Enunciat
Termini de resposta tancat
|
8
|
4 punts |
11 de desembre
|
21 de desembre
|
Enunciat
Termini de resposta tancat
|
9
|
4 punts
|
11 de desembre
|
21 de
desembre |
Enunciat
Termini de resposta tancat
|
| 10 |
(**)
(7 punts) |
19 de desembre |
9 de gener
|
Enunciat
Termini de resposta tancat
|
| 11 |
(**)
(7 punts) |
19 de desembre
|
9 de gener |
Enunciat
Termini de resposta tancat. Concurs acabat!!!
|
|
(*)
Si la resposta numèrica d'un problema s'envia correctament al
segon
intent la puntuació atorgada serà la meitat que si es fa al primer
intent..
(**)Entre parèntesis s'indica el màxim que es podrà atorgar per
l'explicació.
|
Dades estadístiques
Inscripció i problema 0
- 183 inscripcions
- 168 encerts, 156 al primer intent i 12 al segon
Problema 1
- 135 respostes
- 107 encerts, 84 al primer intent i 23 al segon
Problema 2
- 126 respostes
- 119 encerts, 116 al primer intent i 3 al segon
Problema 3
- 115 respostes
- 112 encerts, 97 al primer intent i 15 al segon
Problema 4
- 116 respostes
- 114 encerts, 108 al primer intent i 6 al segon
Fins ara hi ha 55 concursants amb encert de totes les respostes al primer intent
Problema 5
- 105 respostes
- 100 encerts, 93 al primer intent i 7 al segon
Problema 4
- 90 respostes
- 75 encerts, 68 al primer intent i 7 al segon
Fins aquí hi havia 36 concursants amb encert de totes les respostes al primer intent
Problema 7. Les respostes han estat avaluades per un equip de set professores i professors, universitaris, o de secundària, o jubilats . S'han tingut molt en compte les indicacions que ja s'havien publicat pel que fa a l'aspecte eminentment conceptual del problema. La valoració global és molt positiva, amb una mitjana de 3,95 punts sobre 7.
- 56 respostes
- 13 valoracions en l'interval [6, 7]
- 5 valoracions en l'interval [5, 6)
- 10 valoracions en l'interval [4, 5)
Problema 8
- 64 respostes
- 56 encerts, 42 al primer intent i 14 al segon
Problema 4
- 57 respostes
- 49 encerts, 42 al primer intent i 7 al segon
Hi ha hagut 19 concursants amb encert de tots els problemes de resposta concreta al primer intent
Després de la valoració dels problemes de resposta concreta i el problema 7..
- Hi ha un concursant amb la puntuació màxima de 34 punts
- Hi ha uns altres 9 concursants amb més de 33 punts (puntuació en l'interval [33,2 , 33,9])
- Hi ha uns altres 5 concursants amb més de 31 punts (puntuació, def fet, en l'interval [31,9, 32,9])
i per això cal felicitar el conjunt de participants que han anat seguint la participació en el concurs.
Problema 10. Les respostes han estat avaluades per un equip de quatre persones.
La valoració global és positiva, per ser un dels problemes finals
que es considera que han de ser decisius, amb una mitjana de 3,6 punts
sobre 7.
- 34 respostes
- 7 valoracions en l'interval [6, 7]
- 1 valoració en l'interval [5, 6)
- 7 valoracions en l'interval [4, 5)
Problema 11. Les respostes han estat avaluades per un equip d'unes altres quatre persones.
La valoració global també és molt positiva amb una mitjana, excel·lent, de 4,4 punts
sobre 7.
- 28 respostes
- 10 valoracions en l'interval [6, 7]
- 3 valoracions en l'interval [5, 6)
- 5 valoracions en l'interval [4, 5)
Consideracions sobre els problemes "d'explicar"
Previ: El
concurs es proposa com una activitat individual per
a alumnes dels
nivells
indicats. És clar que la comissió organitzadora també valora
molt positivament que les propostes de problemes serveixin per al
treball en equip. Tanmateix, a l'hora de redactar el raonament que
porta a la solució del problema és imprescindible que en la redacció i
la presentació s'observi una tasca individual. Sent així, si dos
concursants envien el mateix fitxer PDF no entrarà en
consideració per a l'avaluació. Quan dues persones, sense copiar,
redacten la solució a un problema sempre hi haurà aspectes que
diferenciaran una explicació de l'altra, encara que abans ho hagin
comentat entre elles.
Sobre l'avalaució dels problemes "d'explicar" i l'assignació de puntuacions
- Cadascun
dels problemes l'avaluaran quatre o cinc persones,
professores o professors universitaris o de secundària, en actiu o
jubilats. A partir dels criteris generals que s'apliquen en concursos
de resolució de problemes matemàtics, cada persona aporta el seu propi
punt de vista i posa la seva puntuació. Després es fa la mitjana de puntuacions i s'arronodeix, cap a dalt, al primer decimal.
- Per als criteris d'avaluació es té en compte com a idea bàsica la que s'indica en les instruccions per a la tramesa del document de resposta, a saber: :
- Cal redactar ben clarament la solució del problema i,
tan detallat com sigui possible, i alhora precís, un camí de raonament
que porti a la solució indicada.
- L'absència
total o molt accentuada de redacció (cosa que es pot observar en
determinades respostes) s'entèn que no s'adiu amb la indicació
anterior. Així mateix una excessiva faramalla en els prolegòmens de
l'explicació o l'ús de recursos excessivament sofisticats es pot
entendre com una pèrdua de precisió.
- Hem
de pensar que aquestes respostes s'envien a un concurs, que és una
situació ben diferent d'un "examen escolar". És a dir que si dos
participants fan raonaments semblants, però un ho explica de manera més
completa, concreta i precisa que l'altre, o amb raonaments conceptualment més interessants, la comissió avaluadora
tindrà una tendència a posar-li més punts. En aquest sentit podem
afegir que la subtil diferència entre un 6,8 o un 6,9 o un 7 es
pot considerar una diferència de puntuació "a efectes de desempats", i
que en concursos com aquest una puntuació de 6 o més ja s'ha de
considerar una valoració ben bona.
Sobre el problema del pentàgon regular i la raó àuria
La formulació de l'enunciat palesa de manera clara que vol
aportar idees sobre la raó àuria i la seva "presència" destacada en el
pentàgon regular.
Atenent a les consideracions generals que heu pogut llegir, aquesta
idea es tindrà en compte, de manera essencial, en l'avaluació del
problema 7.
Potser val la pena comentar que 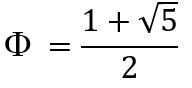 no
es pot considerar una definició del nombre auri; n'és, només el valor
exacte. Convé exposar la definició a partir de la proporció, en
geometria, i la definició algebraica que se'n dedueix.
Es pot arribar a la solució del problema fent ús de la
trigonometria, amb els valors exactes de les raons trigonomètriques dels
angles lligats al pentàgon regular (108º, 72º, 36º) però la deducció
d'aquests valors exactes porta implícit l'ús de la raó àuria. Per això
si algú opta per aquesta línia de treball (que s'ha de considerar ben bé "segona
opció" pel que fa a la valoració) haurà d'incloure la demostració
dels valors exactes indicats.
De fet molts problemes que es poden fer "per trigonometria" es
poden fer de manera "més elegant" (aspecte a valorar en un concurs)
fent ús de la semblança de triangles. Aquesta afirmació és del
tot clara, si es pensa en el paper fonamental de la semblança per a la
definició de les raons trigonomètriques!!!... i en el cas que ens ocupa
pot passar perfectament que per a la demostració dels valors exactes de
les raons trigonomètriques indicades calgui fer el raonament a partir
del que es demana en el problema i aleshores queda encara més clar que
fer servir directament les raons trigonomètriques serà una línia de
treball poc valorada.
www.cangur.org
|


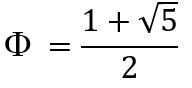 no
es pot considerar una definició del nombre auri; n'és, només el valor
exacte. Convé exposar la definició a partir de la proporció, en
geometria, i la definició algebraica que se'n dedueix.
no
es pot considerar una definició del nombre auri; n'és, només el valor
exacte. Convé exposar la definició a partir de la proporció, en
geometria, i la definició algebraica que se'n dedueix.