Informació sobre el
problema 7- Solució comentada
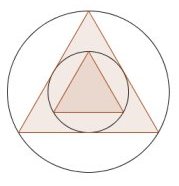
L'àrea del primer triangle és igual a quatre vegades l'àrea del segon.
 - El Fòrum s'anima!!! La
participant Laura Roigé (Oriol Martorell, Barcelona) ens ha
enviat una solució per aquest problema que creiem interessant publicar
perquè, segurament, la trobareu molt encertada.
Comparant-ho amb la solució que s'havia publicat (que teniu més
avall comentada) ens diu:
També
es podia fer de manera més fàcil girant el triangle interior. Si li fem
una rotació de 180º es veu a simple vista que és una quarta part del
triangle exterior.

Excel·lent
manera de veure la solució del problema. Aprofitarem per comentar,
des de la comissió, quelcom que haureu de tenir en compte per als dos
últims problemes, dels quals ja sabeu que es demanarà l'explicació.
Es tracta de "la vista"
que convé sempre raonar. En aquest cas es podia justificar dient que el
cercle inscrit al primer triangle equilàter té com a punts de tangència
els punts mitjans dels costats, que formen un nou triangle equilàter
que serà el segon triangle de l'enunciat. Que els costats del
segon triangle són la meitat dels del primer. I que, doncs, l'àrea és
la quarta part.
- La solució proposada per la comissió és aquesta:
Els
dos cercles que dibuixem són el cercle circumscrit i el cercle inscrit
al primer triangle equilàter que, és clar, tenen el mateix centre, que
és el centre del triangle equilàter (baricentre, circumcente, incentre,
ortocentre, punt de Fermat,...).

Com que el baricentre divideix la mitjana per la tercera part ja
veieu que el radi del cercle circumscrit a un triangle equilàter és el
doble del radi del cercle inscrit. Així
doncs els dos triangles que considerem son triangles equilàters
inscrits en dos cercles que el radi d'un és el doble del radi de
l'altre. El costat d'un triangle també serà el doble del de l'altre i,
per tant, l'àrea del gran serà el quàdruple de l'àrea del petit.
- Aquesta
propietat del baricentre és molt interessant...i tornant als "problemes
explicats", es podria donar com a un fet conegut? Sï!
Ara bé, per si no teníeu present aquesta
propietat del baricentre, es dona una possible explicació del fet que el radi del cercle circumscrit a un triangle equilàter és el
doble del radi del cercle inscrit. En la figura següent hi hem acolorit
dos triangles semblants (rectangles amb un angle de 30º).

Un
d'ells (el verd) té per hipotenusa el costat del triangle i un catet
n'és la
meitat; així es raona que en un triangle rectangle amb un angle de 30º
el catet oposat a l'angle de 30º és la meitat de la hipotenusa. Si ja
heu estudiat triogonometria aquest fet és el que es tradueix dient que
sin(30º) = 1/2.
Així el triangle blau també tindrà la hipotenusa (radi del
cercle circumscrit) igual al doble d'un catet (radi del cercle incrit).
És clar que la solució de la Laura és clara i concreta... perfecta!
Però
ho havíem volgut aprofitar per explicar la propietat del baricentre i
la del catet oposat a un angle de 30º i la hipotenusa.
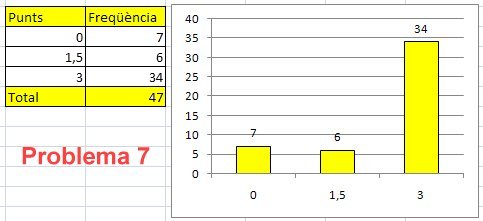
- Aquest era un problema
de 3 punts (encert al primer intent) o de 1,5 punts (encert al segon
intent).
Les
dades:
Enllaç a un formulari per enviar els
vostres comentaris
|