Com a segona part de l'activitat haureu d'enviar un document
.PDF amb el raonament que us ha fet arribar al disseny de la
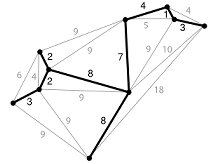
connexió minial entre els sis punts donats i també una explicació de
l'apartat següent.
c) Expliqueu amb detall en quina zona (o en quines zones) pot
estar situat un setè punt G perquè la connexió minimal en el
conjunt dels set punts A, B, C, D, E, F i G estigui formada pels segments que ja teníem en la connexió minimal dels sis punts A, B, C, D, E i F i un
altre segment, que naturalment unirà el punt nou amb un dels sis punts del
conjunt inicial.
Tindreu a la web un formulari per enviar un document PDF amb l'explicació
raonada de les solucions als apartats a) b) i c)
En altres circumstàncies es tracta de connectar punts però sense que,
necessàriament s'hagin de fer servir els segments que uneixen dos dels
punts del conjunt i de manera que es poden introduir nous punts per a
algunes connexions.
En el cas d'un triangle el punt que té la propietat que la suma de
distàncies d'aquest punt als tres vèrtexs del triangle és mínima es
coneix com a punt de Fermat. En concret aquesta distància és sempre més
petita que la suma de dos costats del triangle i, per tant en problemes
de distància mínima s'ha de tenir molt en compte.
d) Dissenyeu un conjunt de segments (que poden tenir extrems en
punts que no siguin del conjunt) que permeti connectar els sis
punts A, B, C, D, E, F, donats com a dades en aquest problema, de manera que la suma de distàncies sigui mínima.
Tindreu a la web un formulari per enviar, independentment d el'anterior, un document PDF
amb l'explicació d'aquest apartat del punt de Fermat
 amb
el
suport de
amb
el
suport de